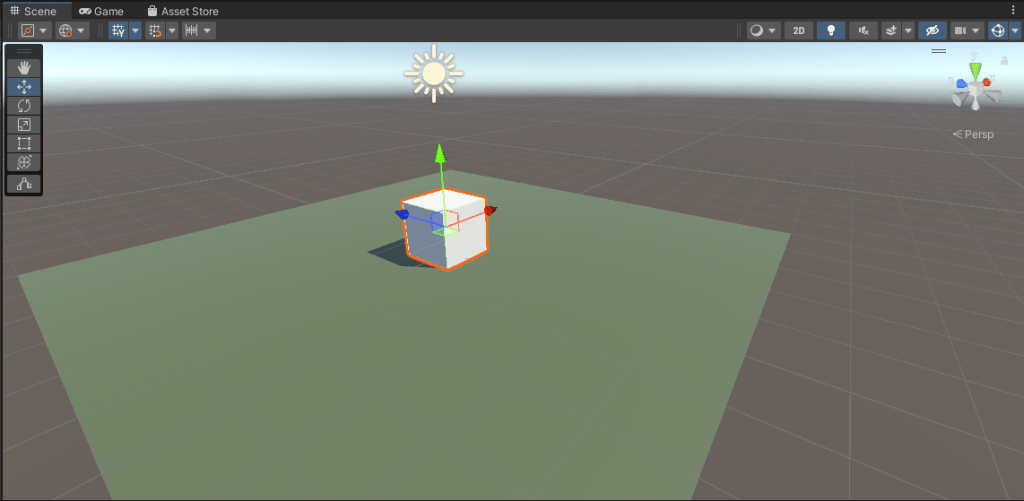
This week we took our cube and made it vaguely more spaceship-shaped by moving it up to (0, 2, 0) and resizing it to (5, 1, 4). We also took our ground plane and scaled it to (10, 10, 10). Now it looks vaguely more like a flying craft than before!
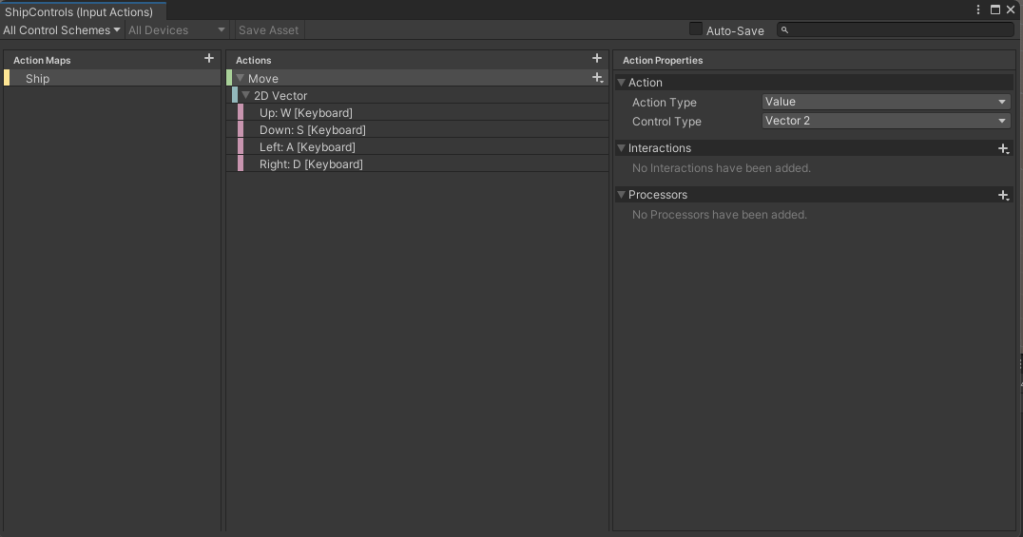
The ship controls still work as before. WASD move the ship horizontally over the ground and there’s no vertical movement. To make it look more like a flying craft, we’d like it to bank (aka. tilt over) as it moves horizontally. That’s going to take a bit of figuring out.
Angles in Unity
Let’s take a little aside to talk about angles in Unity.
In the Unity Inspector we see three numbers for a transform’s rotation. These numbers represent rotations around the X, Y and Z axis respectively. This way of storing a rotation is known as “Euler angles”. It seems simple and straightforward and, if you’re rotating around just one of the X,Y or Z axes, it is, but for complex rotations it actually has a lot of problems. The order in which you apply the rotations matters. If you rotate first in X then Y and the Z, you get one orientation, but choose a different order and you’ll get something different. It’s ambiguous.
Look at these two boxes. Each are rotated by 90degrees around the X and Z axis but in a different order. They end up in completely different orientations:
Rotations internally in Unity are stored using a special variable called a Quaternion. Euler angles can easily be converted to Quaternions and back again. Quaternions store the axis that the object rotates around and the amount of the rotation. It’s completely unambiguous with no order to worry about.
When we code, we use Quaternions for rotations because that’s what Unity uses.
Variables for Ship Tilt
In ShipControls.cs we add two variables TiltSpeed and TiltLimit to control banking. TiltLimit represents the amount of degrees we’re going to bank as we move horizontally and TiltSpeed is how quickly we can change angle. We don’t want the craft immediately going from tilting one direction to tilting the other – we want a smooth change of rotations. That will look a lot better.
public float TiltSpeed = 10.0f;
public float TiltLimit = 10.0f;
Because these are public properties, we see them appear in the inspector for Ship Controller.
Determining What Tilt We Should Have
Tilt is dependent on the user input. If the user is pressing right, we should be titled to the right. If the user is pressing left, we should be tilted to the left. If the user isn’t pressing left or right, we should be level.
In the Update() function in ShipControls.cs we add this code near the top:
float tiltTarget = 0;
if (moveInput.x < 0)
tiltTarget = TiltLimit;
else if (moveInput.x > 0)
tiltTarget = -TiltLimit;
Quaternion targetRotation = Quaternion.Euler(tiltTarget, 0, 0);
So depending on user input, tiltTarget will either be 0, TiltLimit or -TiltLimit (note the minus). We then turn this into a Quaternion representing this amount of a rotation around the X axis.
Moving Smoothly Between Rotations
How do we move smoothly between two rotations, namely the rotation we’re at and the rotation we want to be at?
There’s a general concept called “linear interpolation” for finding a value some proportion of the way between two other values. Let’s imagine a trivial example; if our numbers were 0 and 10 then the number 50% of the way (aka. half) between these would be 5. In Unity linear interpolation is known as “Lerp” and it can be used not just for simple numbers but for Vector3’s (representing positions and directions) and Quaternions (representing rotations) too.
For Quaternions, Unity has a special “Lerp” that works really well for rotations called Quaternion.Slerp(). “Slerp” stands for Spherical liner interpolation. Not a function name you’ll quickly forget. So to “Slerp” between the angle we’re currently at and the angle we’d like to be at, we need to know what proportion of that change we can make this frame. Here’s how we calculate that proportion:
- Find the angular different between the rotation we’re at and the rotation we’d like to be at
- Calculate how long, given the speed we’ve specified for changing angle, it would take to fully make that change in rotation
- Calculate, given the time since the last frame, what proportion of that change we can actually make (it will be just a small bit of the change).
Here’s what the code looks like:
float rotationDiff = Quaternion.Angle(targetRotation,
transform.rotation);
float timeToFullyRotate = rotationDiff / TiltSpeed;
float rotationProportion = Time.deltaTime / timeToFullyRotate;
Finally we actually set the transform’s rotation using Slerp(), the rotation we’re at, the rotation we’d like to be at and the proportion of the change that we’ve calculated:
transform.rotation = Quaternion.Slerp(transform.rotation,
targetRotation,
rotationProportion);
Tuning the Variables
Testing the ship control code we found that good values for the variables were as follows:
| Move Speed | 50 |
| Tilt Speed | 100 |
| Tilt Limit | 30 |
We also noted that any values entered in the inspector override defaults in the code.
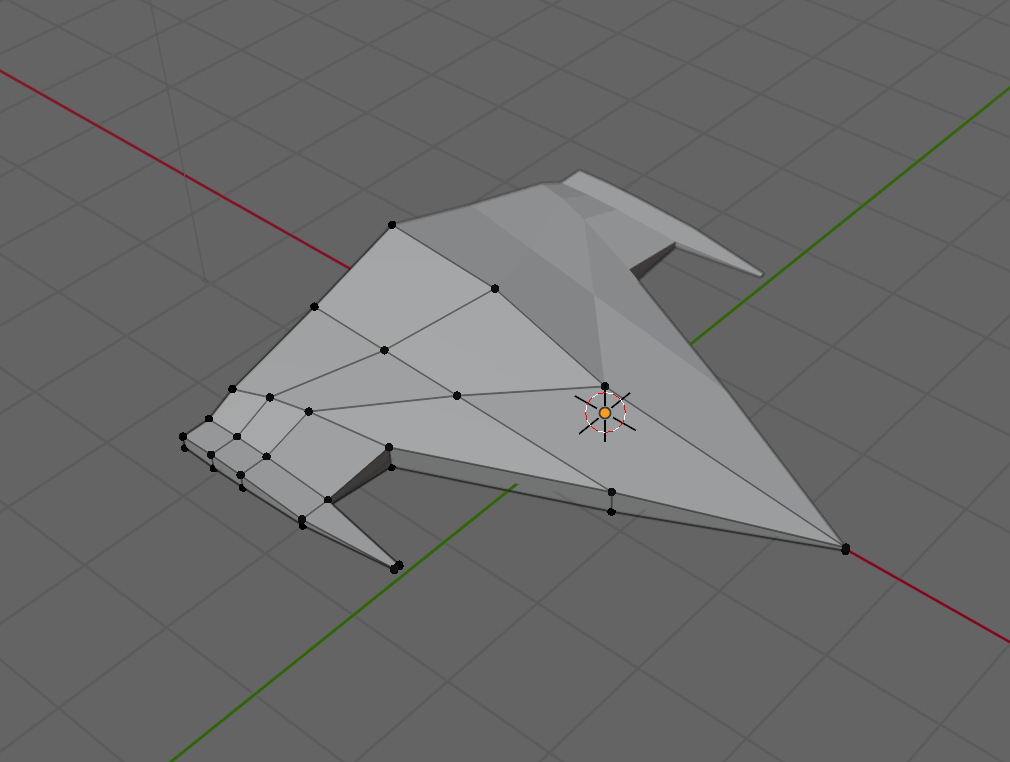
Simple Blender Spaceship
We started on a simple spaceship model in Blender, using the proportions of our cube in Unity as a guide [5m x 1m x 4m].
This was mine, but everyone had their own take. If anyone wants to download mine, it can be found here on our Teams site. If you’re not a member of our Teams site yet, get in touch to be added.
When we return after our break, we’ll look to texture this model and export it from Blender and import it into Unity.
Getting the Code
All the code we’re made this year is on our GitHub. It can be found here. If you don’t have the latest version of our code before any session, use the green Code button on that page to get the “Download ZIP” option which will give you a full copy of all code we’ll be writing this year.